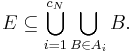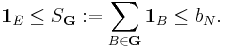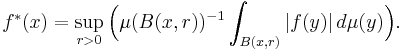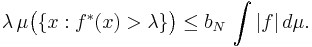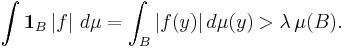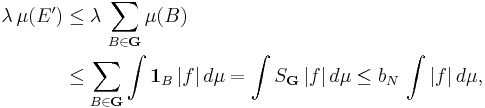Besicovitch covering theorem
In mathematical analysis, a Besicovitch cover, named after Abram Samoilovitch Besicovitch, is an open cover of a subset E of the Euclidean space RN by balls such that each point of E is the center of some ball in the cover.
The Besicovitch covering theorem asserts that there exists a constant cN depending only on the dimension N with the following property:
- Given any Besicovitch cover F of a bounded set E, there are cN subcollections of balls A1 = {Bn1}, …, AcN = {BncN} contained in F such that each collection Ai consists of disjoint balls, and
Let G denote the subcollection of F consisting of all balls from the cN disjoint families A1,...,AcN. The less precise following statement is clearly true: every point x ∈ RN belongs to at most cN different balls from the subcollection G, and G remains a cover for E (every point y ∈ E belongs to at least one ball from the subcollection G). This property gives actually an equivalent form for the theorem (except for the value of the constant).
- There exists a constant bN depending only on the dimension N with the following property: Given any Besicovitch cover F of a bounded set E, there is a subcollection G of F such that G is a cover of the set E and every point x ∈ RN belongs to at most bN different balls from the subcover G.
In other words, the function SG equal to the sum of the indicator functions of the balls in G is larger than 1E and bounded on RN by the constant bN,
Application to maximal functions and maximal inequalities
Let μ be a Borel non-negative measure on RN, finite on compact subsets and let f be a μ-integrable function. Define the maximal function  by setting for every x (using the convention
by setting for every x (using the convention  )
)
This maximal function is upper semicontinuous, hence measurable. The following maximal inequality is satisfied for every λ > 0 :
- Proof.
The set Eλ of the points x such that 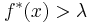 clearly admits a Besicovitch cover Fλ by balls B such that
clearly admits a Besicovitch cover Fλ by balls B such that
For every bounded Borel subset E´ of Eλ, one can find a subcollection G extracted from Fλ that covers E´ and such that SG ≤ bN, hence
which implies the inequality above.
When dealing with the Lebesgue measure on RN, it is more customary to use the easier (and older) Vitali covering lemma in order to derive the previous maximal inequality (with a different constant).
References
- Besicovitch, A. S. (1945), "A general form of the covering principle and relative differentiation of additive functions, I", Proceedings of the Cambridge Philosophical Society 41 (02): 103–110, doi:10.1017/S0305004100022453.
- "A general form of the covering principle and relative differentiation of additive functions, II", Proceedings of the Cambridge Philosophical Society 42: 205–235, 1946.
- DiBenedetto, E (2002), Real analysis, Birkhäuser, ISBN 0-8176-4231-5.
- Füredi, Z; Loeb, P.A. (1994), "On the best constant for the Besicovitch covering theorem", Proceedings of the American Mathematical Society 121 (4): 1063–1073, http://links.jstor.org/sici?sici=0002-9939(199408)121%3A4%3C1063%3AOTBCFT%3E2.0.CO%3B2-W.